Markov Chains

Quick Navigation:

• Markov Chains Definition
• Markov Chains Explained Easy
• Markov Chains Origin
• Markov Chains Etymology
• Markov Chains Usage Trends
• Markov Chains Usage
• Markov Chains Examples in Context
• Markov Chains FAQ
• Markov Chains Related Words

Markov Chains Definition

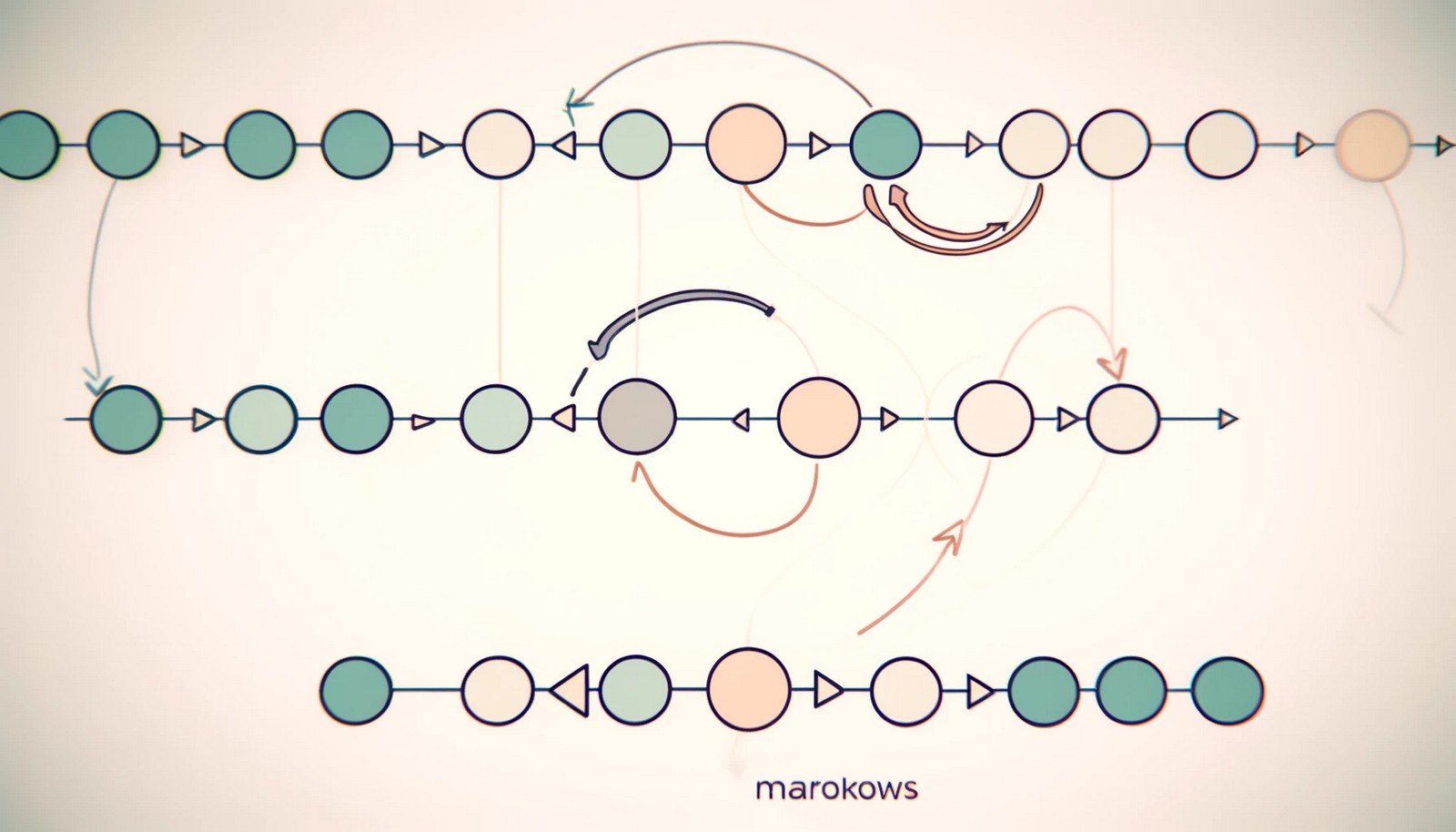
Markov Chains are mathematical systems that transition from one state to another within a finite set of states, where each transition depends only on the current state and not the sequence of events that preceded it. This “memoryless” property simplifies the analysis of processes by reducing dependency on prior states. In technical terms, Markov Chains are stochastic models describing a sequence of events, with a probability distribution governing the likelihood of moving between states. Common applications include prediction algorithms in finance, genetics, and game theory.

Markov Chains Explained Easy

Imagine you're playing a game where you roll a dice, and every roll determines which step you’ll move to next. You don’t need to remember previous rolls—just the result of the current one to decide your next move. Markov Chains work like this: each step (or "state") only relies on the last one, not on all past steps. It's like always knowing where to go next, just by looking at where you are now.

Markov Chains Origin

The concept of Markov Chains was introduced by the Russian mathematician Andrey Markov in the early 20th century. Originally used to study linguistic patterns, the theory has since evolved and is now widely applied in various fields, including statistics, economics, and computer science.

Markov Chains Etymology

The term "Markov Chain" is named after Andrey Markov, who pioneered this concept in probability theory to explore random processes.

Markov Chains Usage Trends

In recent years, Markov Chains have gained traction in data-driven fields like machine learning, finance, and linguistics. The rise of AI has highlighted the importance of predictive models, making Markov Chains indispensable in areas where probability-based predictions are crucial, such as speech recognition, stock price modeling, and web page ranking algorithms.

Markov Chains Usage

• Formal/Technical Tagging:
  - Stochastic Processes
  - Probability Theory
  - Predictive Modeling
• Typical Collocations:
  - "Markov Chain model"
  - "Markov Chain analysis"
  - "finite Markov Chain"
  - "state transition matrix in Markov Chains"
  
  

Markov Chains Examples in Context

• In finance, Markov Chains help predict stock prices by modeling price movements based solely on current market conditions.
• Text-based applications, like predictive text on smartphones, rely on Markov Chains to guess the next word based on the current word alone.
• In genetics, Markov Chains model sequences in DNA, where each nucleotide is predicted based on the preceding nucleotide.
  
  

Markov Chains FAQ

• What is a Markov Chain?
  A Markov Chain is a mathematical model that describes a system where the next state depends only on the current state.
• How are Markov Chains used in AI?
  Markov Chains are used in AI for predictive tasks, such as natural language processing and recommendation systems.
• What fields commonly apply Markov Chains?
  Common fields include finance, biology, linguistics, and game theory.
• What makes Markov Chains “memoryless”?
  The memoryless property means each state transition depends only on the current state, not past states.
• Can Markov Chains model random processes?
  Yes, they are often used to model random processes where each event depends solely on the present condition.
• What’s the difference between a finite and infinite Markov Chain?
  A finite Markov Chain has a limited number of states, while an infinite one has an unlimited number of possible states.
• Why are Markov Chains useful in finance?
  They predict market trends by analyzing transitions based on current data, helping to forecast price movements.
• Are Markov Chains applicable in genetics?
  Yes, they model sequences in DNA and RNA, helping to predict genetic patterns.
• What’s a state transition matrix?
  It’s a matrix that shows probabilities of moving from one state to another in a Markov Chain.
• Do Markov Chains apply to weather prediction?
  Yes, they model weather patterns by predicting transitions, such as moving from sunny to rainy conditions.
  
  

Markov Chains Related Words

• Categories/Topics:
  - Probability Theory
  - Stochastic Processes
  - Predictive Analytics
  
  

Did you know?
Markov Chains were first applied to linguistic patterns. Andrey Markov analyzed letter sequences in Alexander Pushkin's poetry to study dependencies in language—a unique intersection of math and literature that marked the beginning of Markov Chain applications.

Authors | Arjun Vishnu | @ArjunAndVishnu

 

PicDictionary.com is an online dictionary in pictures. If you have questions or suggestions, please reach out to us on WhatsApp or Twitter.

I am Vishnu. I like AI, Linux, Single Board Computers, and Cloud Computing. I create the web & video content, and I also write for popular websites.

My younger brother, Arjun handles image & video editing. Together, we run a YouTube Channel that's focused on reviewing gadgets and explaining technology.