Linear Regression

Quick Navigation:

• Linear Regression Definition
• Linear Regression Explained Easy
• Linear Regression Origin
• Linear Regression Etymology
• Linear Regression Usage Trends
• Linear Regression Usage
• Linear Regression Examples in Context
• Linear Regression FAQ
• Linear Regression Related Words

Linear Regression Definition

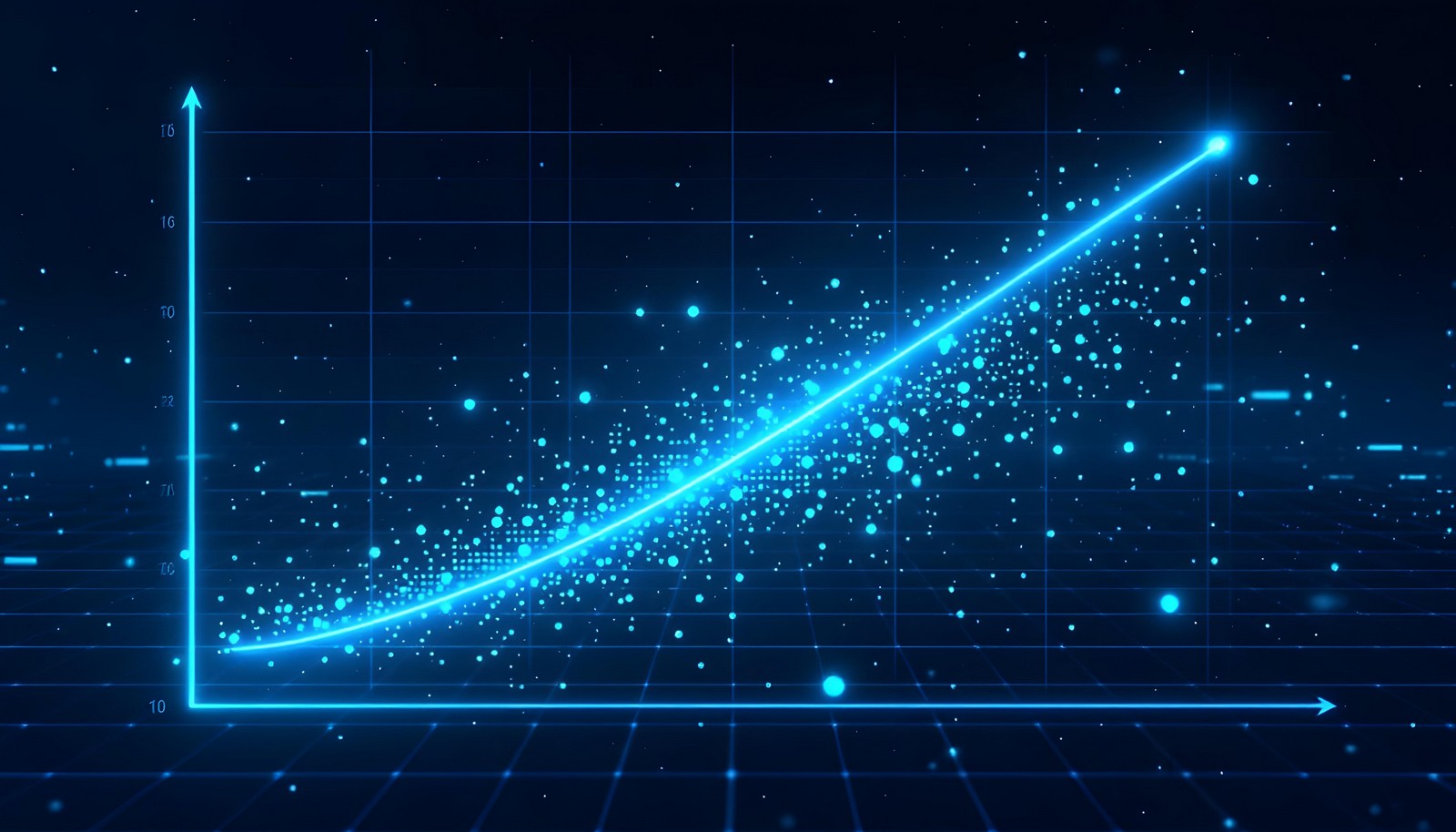
Linear regression is a statistical method used to model the relationship between a dependent variable and one or more independent variables by fitting a linear equation to observed data. This technique assumes that the relationship between variables is linear, making it useful for predicting values and understanding data patterns. Key applications include trend analysis, forecasting, and determining variable impacts in fields like economics, biology, and social sciences.

Linear Regression Explained Easy

Imagine you have a bunch of points on a piece of paper. Now, you try to draw a line that goes as close as possible to all those points. That line shows you the general direction the points are moving in, helping you guess where future points might be. Linear regression does just that: it finds a line that best fits data points to help predict future outcomes.

Linear Regression Origin

The origin of linear regression can be traced back to the late 1800s when Sir Francis Galton explored the concept of "regression to the mean." This foundational concept evolved with contributions from Karl Pearson, who developed correlation methods that form the basis of modern regression analysis.

Linear Regression Etymology

The term “regression” originates from the Latin word "regressus," meaning "a return," reflecting the tendency of variables to regress toward the mean in statistical analysis.

Linear Regression Usage Trends

Linear regression remains one of the most widely used statistical methods due to its simplicity and interpretability. It has gained traction in modern data science and machine learning, where it’s often applied to understand trends, forecast values, and build baseline predictive models. The rise of big data and analytics has further expanded its utility across diverse fields, from finance to public health.

Linear Regression Usage

• Formal/Technical Tagging:
  - Statistical Modeling
  - Machine Learning
  - Predictive Analysis
• Typical Collocations:
  - "linear regression model"
  - "least squares method"
  - "predictive accuracy in linear regression"
  - "interpreting regression coefficients"
  
  

Linear Regression Examples in Context

• Economists use linear regression to forecast trends like inflation rates by examining past economic data.
• In healthcare, linear regression models help predict the impact of various risk factors on patient health outcomes.
• Marketing analysts use it to study relationships between advertising expenditure and sales.
  
  

Linear Regression FAQ

• What is linear regression?
  Linear regression is a statistical technique used to understand the relationship between a dependent and one or more independent variables by fitting a straight line to data.
• Why is linear regression important in data analysis?
  Linear regression helps identify patterns, predict trends, and understand the impact of different variables on a target outcome.
• What is the least squares method?
  The least squares method minimizes the sum of squared differences between observed and predicted values, helping find the best-fit line in linear regression.
• What’s the difference between simple and multiple linear regression?
  Simple linear regression models one independent variable, while multiple linear regression includes two or more predictors to explain the dependent variable.
• How is linear regression used in machine learning?
  Linear regression serves as a fundamental supervised learning algorithm for regression tasks, where it predicts continuous outcomes based on input variables.
• What are the assumptions of linear regression?
  Key assumptions include linearity, independence, homoscedasticity, and normally distributed residuals.
• Can linear regression handle non-linear relationships?
  Standard linear regression cannot, but polynomial regression or other transformations can model non-linear relationships.
• What is multicollinearity in linear regression?
  Multicollinearity occurs when independent variables are highly correlated, potentially distorting regression coefficient estimates.
• How does linear regression handle outliers?
  Outliers can skew results significantly. Various methods, like robust regression, help manage this issue.
• What are some real-world applications of linear regression?
  Applications include economic forecasting, medical outcome prediction, and sales and revenue analysis.
  
  

Linear Regression Related Words

• Categories/Topics:
  - Machine Learning
  - Data Analysis
  - Predictive Modeling
  - Statistical Methods
  
  

Did you know?
Did you know that linear regression is a foundational technique in statistics and data science? It’s one of the simplest and most interpretable models, used across fields for predicting trends and making informed decisions based on data patterns.

Authors | Arjun Vishnu | @ArjunAndVishnu

 

PicDictionary.com is an online dictionary in pictures. If you have questions or suggestions, please reach out to us on WhatsApp or Twitter.

I am Vishnu. I like AI, Linux, Single Board Computers, and Cloud Computing. I create the web & video content, and I also write for popular websites.

My younger brother, Arjun handles image & video editing. Together, we run a YouTube Channel that's focused on reviewing gadgets and explaining technology.